Statics Chapter 2 Question 115

sketchfab

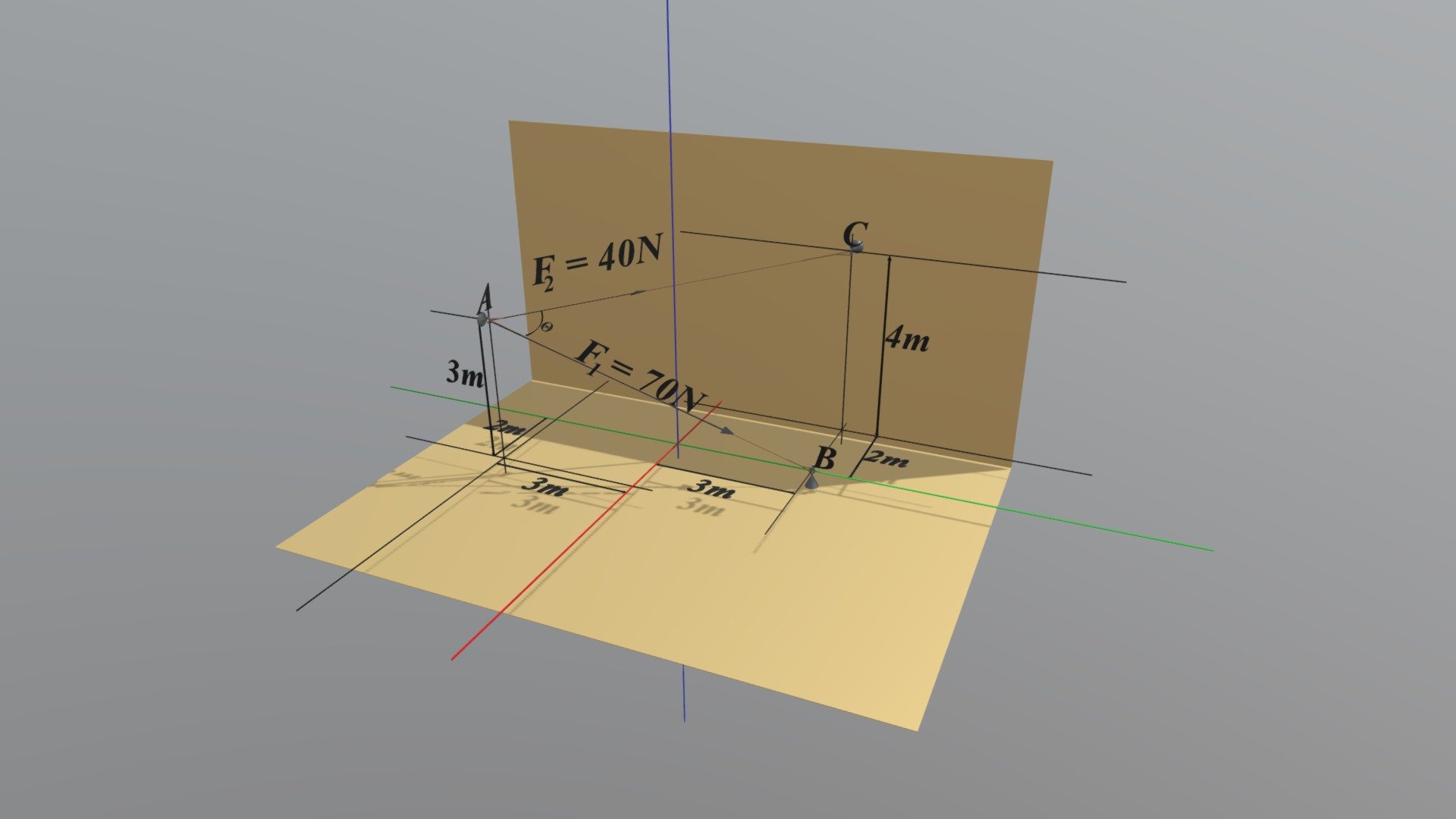
A Student's Guide to Tackling Cartesian Vector Problems with Confidence and Precision In the realm of engineering mechanics, specifically within the context of statics, chapter two serves as a pivotal foundation for understanding complex concepts. Section 2.9 delves into the intricacies of dot products, a crucial aspect that requires diligent comprehension. Question 115, although seemingly straightforward, demands meticulous attention to detail and a thorough grasp of vector operations. To tackle this question with finesse, it's essential to begin by visualizing the problem in three-dimensional space. A diagram, preferably in the form of a 3D Cartesian coordinate system, will serve as an invaluable tool for clarifying relationships between vectors. By representing vectors in their respective dimensions (x, y, z), students can effectively utilize the dot product formula: u · v = |u| |v| cos(θ). This equation highlights the importance of understanding vector magnitude and angle, both critical components in determining the outcome of a dot product operation. As students navigate through this problem, they will find themselves engaged in an exercise that not only demands technical proficiency but also encourages spatial reasoning and visualization. The solution to question 115 hinges on the ability to correctly apply mathematical principles to real-world scenarios. It is here that the significance of mastering vector operations becomes apparent, as it empowers engineers with the tools necessary to tackle a wide range of challenges in statics and beyond.