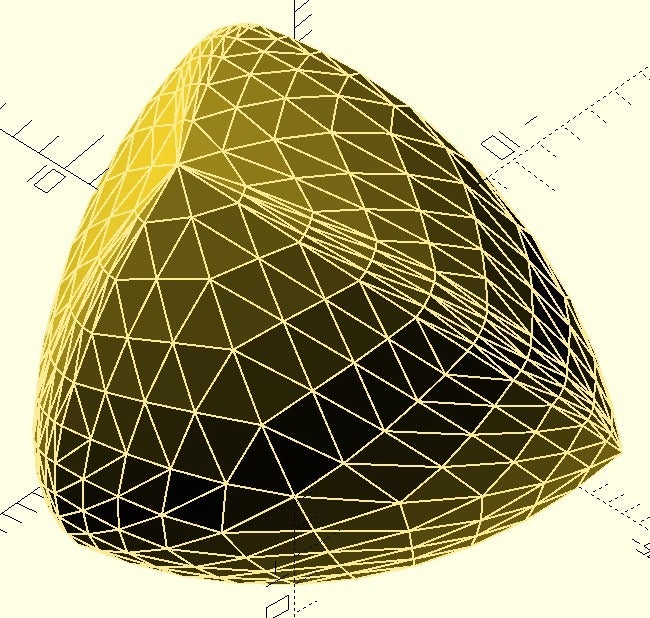
Single Polyhedron Symmetric Spheroform Tetrahedron

prusaprinters

<p>Spheroform with Tetrahedral Symmetry</p> <p>Inspired by Angus one Friday night <a href="https://www.youtube.com/watch?v=fOojOfpcPZM">Ultimate Solids of Constant Width</a>. I thought I would combine the ideas of tetrahedral symmetry and a low poly/fast OpenSCAD implementation.</p> <p>Third attempt following OpenSCAD speed optimisation to it's ultimate conclusion - a single polyhedron. Not sure how I feel about that...</p> <p><a href="http://www.xtalgrafix.com/Spheroform2.htm">More information and Proof</a></p> <h3> Increasing Levels of Detail</h3> <h3> <p class="detail-caption"><strong>segs 1 through 24</strong></p> Mathematical Details</h3> <p><p class="detail-caption"><strong>Roberts 2012</strong></p> <div><p>After examining the <a href="http://www.xtalgrafix.com/Reuleaux/Spheroform%20Tetrahedron.pdf" rel="nofollow">proof by Roberts</a>, we can redefine the required sphere envelope as the set of all points which lie on a line passing through centres of two opposing envelope spheres and intersecting the outer surface of each sphere. This is the actual surface described in the details of Roberts' proof which satisfies the constant width requirement, but I'm not quite convinced that it is the same surface one would obtain from taking the outermost surface of a volume defined by sweeping spheres (looks like it might work out, maximal radius for a given R and angular direction also appears to be a quadratic relationship in R).</p> TLDR: To construct our mesh, we simply iterate over points along opposite (parabolic) envelope centre lines, draw a line through them and extending out by the required radii at each point.</div></p> Category: Math Art