Riemann Spires

thingiverse

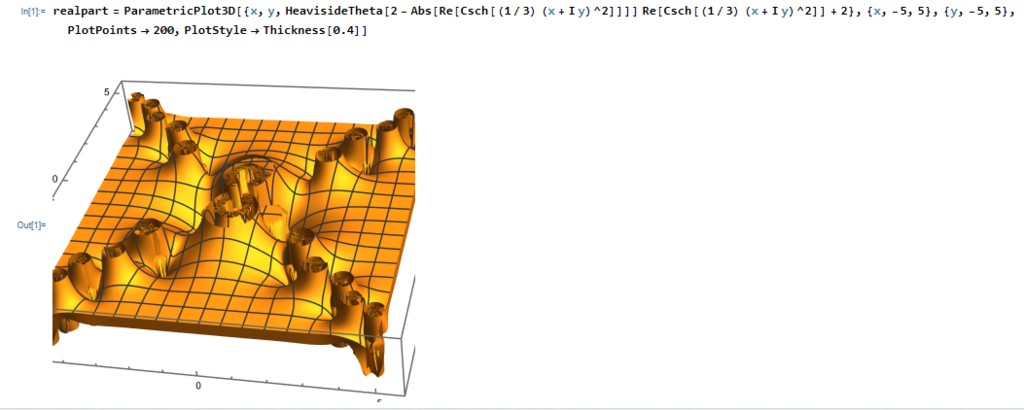
Vincent Vu December 4th, 2021 George Mason University MATH 401: Mathematics through 3D Printing These prints represent the real and imaginary parts of the complex function f(z)=csch((1/3)*z^2). The topic of this week’s print was Riemann Surfaces, which helps us visualize multi-valued functions that are 4-dimensional that would otherwise not be possible. There are many ways to use Riemann Surfaces to represent a complex function, such as having two surfaces for the real and imaginary parts (as I did) f(z) or two surfaces for the modulus and arguments of f(z). I ended up going with the real and imaginary parts for my function since it was tedious but still possible to break into real and imaginary parts while not looking possible to do the other way. The standout of both the real and imaginary surfaces are the spire-like protrusions above and below the base of the surface. These are the poles, which in complex analysis means that the function is undefined at this value and thus values around it diverge towards positive or negative infinity. While the two surfaces behave differently at the origin as expected, I found it odd that both seemed to have the same behavior elsewhere where these poles formed an X shape from the lines y=x and y=-x. To find the exact location of these poles, I did some algebraic manipulation to the equation (work attached in one of the photos) and found that the poles exist at y= ±sqrt(πn/3), x=±sqrt(πn/3), which aligns with our original observations that our poles lay on the lines y=x and y=-x. For the print itself, I ran into a lot of issues with the poles since those values approach infinity, which led to Cura thinking that my z dimensions were some absurdly large number that couldn’t even be reasonably scaled down to fit onto a plate. To workaround this, I ended up using Mathematica’s Heaviside function to make anything that went past 10 to just stay at the base of the surface. This plugged the holes of the surfaces, which was a bummer for me since I would’ve liked to see from one end to the other, but it prevented me from trying to print a file that had an impossible height dimension. There were also some double rings in the poles that were too thin to print for whatever, so we ended up using the Thickness[0.4] from Mathematica’s PlotStyle to close the gap between the rings and make it a fat and printable piece. Finally, we took advantage of the double extruders from the Ultimaker S5 and printed the roof and the floor of the supports with dissolvable filament; this allowed us to use less dissolvable filament while also making it so that once dissolved, the rest of the supports would be detached from the surfaces since the only thing holding them together was the dissolvable supports. Print settings and other details listed below.