Ellipson 13

pinshape

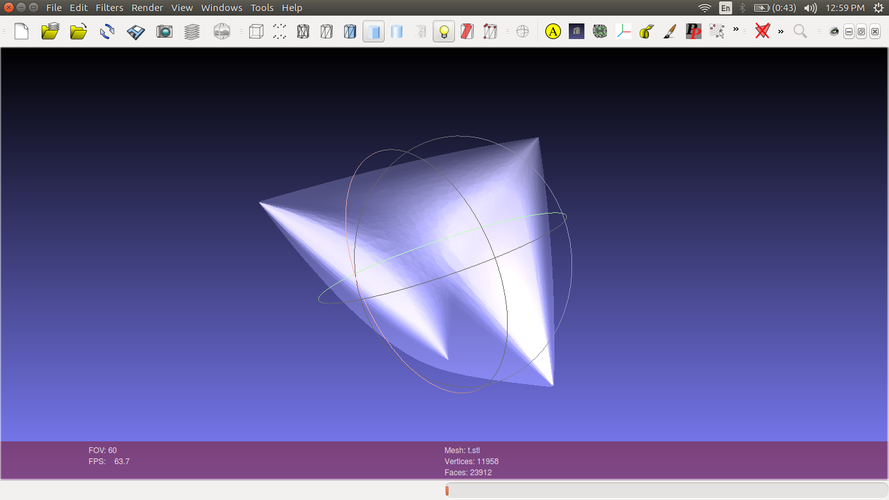
This is an Ellipson, detailed in Norman Wildberger's book "Divine Proportions" , Appendix B. http://wildegg.com/ It reveals points with Descartes coordinates  x,y,z that fulfill this equation: (x+y+z)^2 = 2(x^2+y^2+z^2)+4xyz x,y,z is a "spread triple" of a triangle. For example, for a triangle with sides 3,4,5, the triple is 16/25, 9/25, and 1. If you discover the various spread triples for an enormous number of triangles, you get a three-dimensional surface with coordinates x,y,z, which is called the Ellipson in the above-referenced book. Or in traditional language, for any triangle, take the square of the sine of each angle. You will obtain three numbers x, y, and z that conform to this pattern. If you create a surface of all possible such x y z points, you get the Ellipson. Python code is available here (under the 'antiprism' directory) http://github.com/donbright/pi... The code works by generating 20,000 random triangles in a plane, calculating the three quadrances of each side, then using Wildberger's Cross Law and other Rational Trig laws to solve for the three spreads. The code outputs 3D coordinates (like 0.4, .6,0.9 ) then Antiprism's conv_hull creates a shell as an .off file http://www.antiprism.com Image was made with meshlab using 'glass' shader http://meshlab.sourceforge.net